The tyranny of π

If you get to know me long enough, you’ll find out that I have a thing for numbers. It straddles the border between quirk and obsession. I studied math just a shade beyond the required calculus classes at my university. There was something magical to me about an elegantly written proof, sort of the same way that art aficionados find beauty in paintings. You would think, given my numerophilia, that I would have some warm and special place in my heart for π.

Nope.

This could come off as a hipster grudge against popular irrational numbers (after all, who HASN’T heard of π?), but my lack of love for π goes quite deeper than that. It boils down to the notion that π is a fundamentally flawed number. To see why, travel back in time and remember when you were first introduced to π.

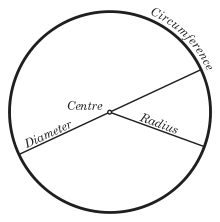
[Image Credit: Optimager via Wikimedia Commons]

 Most likely, you first met it when you learned how to handle circles in middle school math. π is the ratio of the circumference to the diameter. It’s DIAMETER. What mathematical sense does that make? The basic definition of a circle is “a closed plane curve consisting of all points at a given distance from a point within it called the center.” That given distance is the circle’s radius. It makes more sense to change this circle ratio to reflect the importance of the radius. If we divide a circle’s circumference by its radius, we get τ, or tau. Numerically, it’s the same as 2π, approximately 6.28.

It seems trivial to rewrite mathematics over this minute detail. However, once you forget about the high pedestal that π sits upon, you’ll soon realize that τ is a more intuitive number. Flash forward a couple of years, to when you first started delving into trigonometry and came across the unit circle.

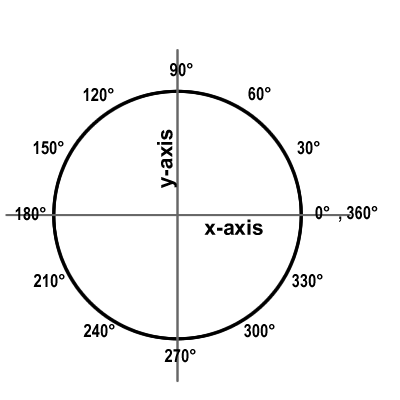
[Image Credit: Phillip Conrad]

A circle is 360 degrees all the way around. Starting from the circle’s rightmost point you travel counterclockwise along the circumference. You can stop at any point along the way, see where you are relative to the center, and figure out the angle. If you’re halfway along the circle, you’re 1/2 x 360 degrees, or 180 degrees. A quarter of the way? 90 degrees. So far, so good.

But degrees don’t play nicely in mathematical functions and formulas. We were always taught to convert the degree measurement into radians. This served as a big stumbling block for a lot of my classmates, as 360 degrees corresponded to 2π radians. Why should a single rotation around the circle correspond to TWICE the number? Replacing π with τ is not only a simpler conversion, but a more intuitive one. One full rotation around is τ radians. Halfway around, at the leftmost point? τ/2, or 180 degrees. Quarter around, at the top? τ/4, or 90 degrees.

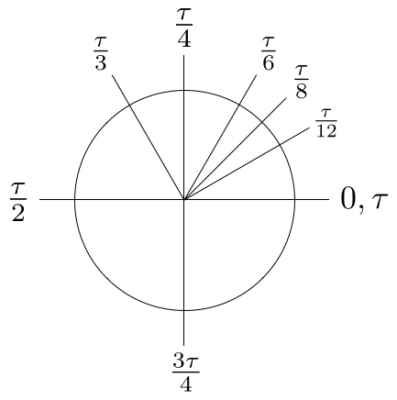
[Image Credit: Michael Hartl]

Making the unit circle easier to visualize eases the student into learning trig. Knowing that the x and y axes of the unit circle correspond to the cosine and sine of the angle formed, it’s easy to quickly reference the special angles that we were taught to memorize. τ/4 is one quarter around the circle, which clearly means the top (in contrast to the less intuitive π/2). It sits at the point (0,1), which means that the sine of τ/4 is 1, while its cosine is 0.

The list of τ’s advantages goes on and on. Michael Hartl, author of the Tau Manifesto, explains it in far more detail than I could. It’s definitely worth checking out if you want to see how τ works for sine waves, calculus, and more advanced math. From a pedagogical perspective, why bother making students go through the extra conversion if their intuition serves them well enough?

So I choose to celebrate Tau Day on June 28th. It doesn’t have the ring of Pi day, nor the tasty desserts associated. But that’s okay. I make my own parties. A handful of ta(u)cos and a pitcher of margarita(u)s. Care to join me in next year’s celebration?