I Just Need Some Spacetime — Separating Twins with Special Relativity
The twin paradox shows how approaching the speed of light alters both time and space
Dan Robitzski • January 11, 2017

They may still share a birthday, but if one of astronaut Mark or Scott Kelly’s missions involved traveling near the speed of light, then he would return having aged less than his brother. [Image Credit: NASA]
Funny things start to happen when you travel near the speed of light. Your perception of the universe changes in some pretty funky ways. But it’s not a trick — your bizarre experiences are just as real as everyone else’s, even if they seem to contradict one another at first glance.
To understand why, let me tell you a story about two twins, one of whom is going to go on an incredible journey through time. That lucky twin is Ulysses; his brother, Homer, likes to stay at home.
Unfortunately for whomever has been planning their joint birthday party, Homer and Ulysses won’t be twins for long. Homer and Ulysses may not be real twins, but physicists have been telling their own versions of the brothers’ story for years.
We’re going to have some fun with Ulysses. And by fun, I mean we’re going to shoot him into space at nearly the speed of light. Ulysses will be visiting Alpha Centauri, our solar system’s closest neighbor at a modest four-and-change light-years away. At the speed of light — almost 671 million miles per hour — the trip would take just over four years. Keep in mind that our friend Einstein famously discovered that nothing can travel faster than light, so Ulysses will only be traveling at nine-tenths light-speed. But that’s still fast enough to see some of our nice, comfortable rules of physics unravel.
The effects of traveling near the speed of light are bizarre, but they’re explained by Einstein’s postulates for special relativity, first devised in 1905. Einstein discovered that the speed of light is constant and the laws of physics remain the same in any inertial reference frame, or any point of view that isn’t accelerating, turning, or being pulled. So all of the same rules that apply to Homer, sitting comfortably at home, also apply to Ulysses’ frame of reference, which moves with him from Earth to Alpha Centauri. Actually, Homer is zipping through the universe as a passenger on Spaceship Earth but we can consider him to be static compared to Ulysses because the earth doesn’t travel nearly as fast as Ulysses’ rocket.
This is all well and good at sensible speeds at which us earthlings go about our business. But as you approach the speed of light, these relations become less intuitive. For instance, if a plane takes off of a moving aircraft carrier, a person watching from the shore will measure its speed differently than someone watching from the carrier. The person on board is moving forwards with the ship, so they will think that the plane is moving that much slower. Both people are correct, and both can use the laws of physics to understand the flight of the plane. However, if you shine a searchlight straight ahead, everybody would measure it as traveling away at the same speed — the speed of light — even if they are moving as well. So where did the observed difference based on one’s speed go?
The answer is that time slows down the faster you move. When you walk past someone on the street, the difference between your speeds produces a tiny fluctuation in time, but the change is so minuscule that you would never notice. Even if you managed to travel at one one-hundredth the speed of light — a speed that’s still totally unattainable by modern spacecraft — you would only measure a thousandth of a percent’s difference when comparing clocks. These aspects of physics are undetectable on a daily basis, where things are relatively slow. But when you start to approach light speed, things get more interesting.
Let’s say that, through his telescope, Homer sees two small meteorites strike the front and back of Ulysses’ ship simultaneously. What does Ulysses see as he sails away from the rear meteorite at close to light speed? Since the speed of light is constant, the light from the front meteorite will reach him sooner than that from the rear. So for Ulysses the front collision happens first, followed quickly by the knock from the rear.
Again, both Homer’s and Ulysses’ perspectives are valid, even though they disagree. What this means is that the laws of physics do not preserve the notion of two events being simultaneous. The order in which you observe events happening depends on your frame of reference.
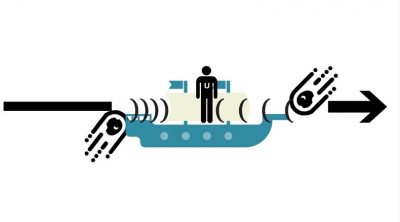
Ulysses is moving so rapidly that if two meteors crashed into his ship, the light waves from the two collisions will reach him at different times. To him, the impacts are not simultaneous. [Image Credit: The artistic mastery of Dan Robitzski]
Light headed back to Earth from the craft will take a specific amount of time to reach Homer’s telescope. Homer can easily work this out because light travels at only one speed. But from Ulysses’ point of view, it’s the Earth, rather than his ship, that’s moving. So he will calculate that the light takes longer to reach Earth because the planet keeps moving away from the light that’s traveling towards it.
The speed of light does not change, so both brothers are right. This means that time is behaving differently for the brothers. For Homer, who is measuring time as it passes on Earth, Ulysses’ trip takes longer than it does for Ulysses in the ship. Again, both brothers are technically correct; they will experience the flow of time differently. Homer will become older than his former twin.
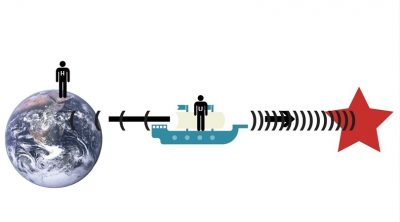
The light waves leave Ulysses’s ship at the speed of light — relative to Ulysses — and head toward a receding Earth. But since time passes more slowly for Ulysses, they arrive at the same time that Homer would calculate base on a moving spaceship and a stationary Earth. [Image Credit: Dan Robitzski]
Still, taking an interstellar trip is no way to cheat death. “There’s no free lunch here,” says Ronald Lasky, an engineer at Dartmouth College who has written about the problem known as the twin paradox. “You can’t do this to live longer.” Ulysses is now younger than Homer, but he hasn’t lived in some sort of suspended youth. Ulysses has simply lived fewer years than his brother has, but to him everything felt like business as usual.
Space, like time, also gets distorted. For Homer, back on Earth, it’s easy to measure how far Ulysses has traveled. He could just hold up his handy four-light-year-long ruler and measure. This time, he technically has the proper measurement because he’s not moving relative to Earth or the distant star. But for Ulysses, determining distance is more complex — he has to calculate how far he’s gone based on the time he’s been traveling and the speed at which he’s moving.
Both brothers agree on the speed, but Ulysses measures time more slowly than Homer, so the trip takes him less time, as we’ve already seen. A shorter trip at the same speed means Ulysses will calculate a shorter distance between Earth and Alpha Centauri. The distance that Ulysses travels — from his perspective — shrinks. His space has been squeezed just as Homer’s time has been stretched. The calculations for the length contraction effect are similar to those for time dilation. At 90 percent light-speed, that four-light-year distance would be just about halved.
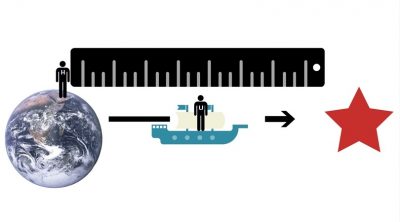
Homer can measure distance whereas Ulysses has to calculate it using distorted time measurements. According to Ulysses, he’s traveled about half the distance that Homer measures. [Image Credit: Dan Robitzski]
The actual paradox comes from Ulysses’ assumption that, looking back at Earth, sees Homer moving away from him and calculates that his now-older brother will end up even younger than he is, as if Homer were the one traveling.
This is a paradox — not a true contradiction of physics — it has an explanation. The key is that Ulysses couldn’t simply bounce off of Alpha Centauri and immediately return home — he would need to slow down, turn around, and then approach Earth. During the U-turn, our adventurous friend was no longer in an inertial reference frame — he was slowing down and speeding back up. His brother, on the other hand, was doing no such thing. This is where the discrepancy happens, if Ulysses accounts for the physics of this turn, he would see that he skips over the extra years his brother measures.
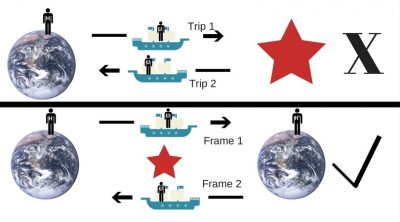
Reference frames are not interchangeable, so to make sense of the paradox one must imagine two separate ships — each with its own frame — that cross paths rather than one that needs to decelerate and turn around. Now each ship represents one of two reference frames through which Ulysses travels. [Image Credit: Dan Robitzski]